A common question in LEGO creations is “how do I build on a diagonal?” If you have studied trigonometry you will know one answer: the Pythagorean triangles, such as the fairly well-known 3-4-5 ratio, will give you a nice diagonal connection on a rectilinear grid such as LEGO provides. Now there’s a new page from the Cactus Brick site that explains these Lego Diagonal Connection Points in a very clear way. Check it out!
Tag: geometry
Track Layout Geometry
Three years ago (on November 21, 2003) I wrote a page on my old site about
Track Layout Geometry showing some of the interesting things you can do with LEGO train track, for example, this method for running track on the 22.5° diagonal:
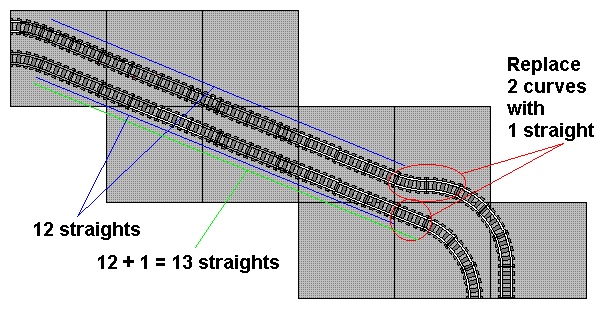
I was browsing my favorite blogs today and noticed that the page got mentioned on Mike Walsh’s blog (link removed, as his site has apparently been compromised). That prompted me to take another look at it, and I decided it really would be better to put it here on the Brickpile site. So I moved that page to this site, and changed the page on the old site to redirect to it with a 5-second delay using JavaScript. Thanks for the link Mike (and sorry for changing it out from under you)!
Road Bridge
In 2003 (or maybe 2002) I built a bridge for the BayLTC train layout. But it wasn’t a train bridge, it was a road bridge (for cars and trucks).
The road pieces came from LEGO’s 6600 Highway Construction set, and the bridge’s structural elements were built of Technic bricks.
Most of the angles in the bridge truss design follow some multiple of the 3-4-5 triangle. This is one of the most useful laws of trigonometry: if you have a triangle with sides 3, 4, and 5, or any multiple of that (such as 30, 40, 50) then they will form a perfect right triangle (a triangle where one of the angles is exactly 90 degrees). Why? Because of the Pythagorean Theorem: in any right triangle, the square of the hypotenuse (the side opposite the 90° angle) is always equal to the sum of the squares of the other two sides. And it so happens that 32 + 42 (9 + 16) is equal to 52 (25).
In LEGO, the 3-4-5 triangle is achieved by attaching pieces in distances of 4-5-6 studs. Why? Because of the “fencepost effect” – if you make the connection on the 1st and 4th stud, that’s actually a distance of 3 (since 4-1=3). The same goes for the 4 and 5 unit length sides. In this model, the center trusses are formed by 3-4-5 triangles scaled up by a factor of 6. So the “4” sides (the vertical) are really 24 (actually 25, because of the fencepost effect) tall. The angled trusses are made by sheer guesswork, however. Luckily, there’s enough slop in LEGO connections to make it not really be necessary to always get it just right. When working on this, I built what I called a “Pythagorometer” – a model of the 3-4-5 triangle at various scales – to try to make the angles work out. I’ll post more about that later.
I recently discovered a batch of pictures of this bridge that had never been posted online, taken at the July 2003 GATS layout. You can see them at a Flickr gallery.


